Module: polyhedron

Source:

Classes

Polyhedron

Members

(static, constant) limit :Object.<{tet:Number, oct:Number, dod:Number, ico: Number}>

Maximum subdivision level without overflowing any buffer (16 bits - 65536).
Type:
  • Object.<{tet:Number, oct:Number, dod:Number, ico: Number}>
Source:

(static, constant) nsegments :Number

Default number of segments (points - 1) for drawing a meridian or parallel.
Type:
  • Number
Source:

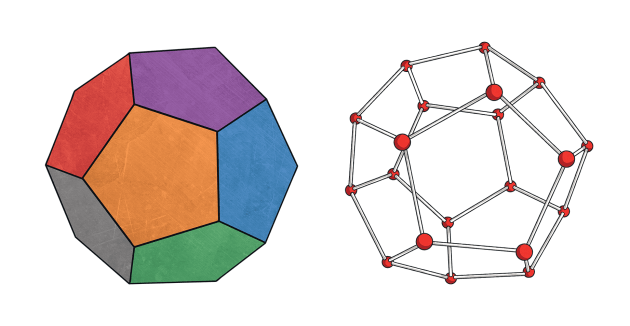
(inner, constant) initialDod :Array.<vec3>

Twenty points of a dodecahedron inscribed in the unit sphere.

Golden Ratio:
  • Φ = (√5+1)/2 = 1.618033988749895
    • 2/Φ = √5 - 1 = 1.2360679774997898
Radius of circunscribed sphere:
  • R = √3 Φ/2 a = 1
Edge length:
  • a = 4R / ((√5 + 1)√3) = 2/Φ R/√3 = R (√5 - 1) / √3 = 0.71364417954618
Vertex coordinates:
  • 1/√3 = 0.5773502691896258
  • 1 / Φ√3 = (√5-1) / (2√3) = 0.35682208977309
  • Φ / √3 = (√5+1) / (2√3) = 0.9341723589627158
The eight vertices of a cube:
  • (±1/√3, ±1/√3, ±1/√3)
The coordinates of the 12 additional vertices:
  • (0, ±(Φ / √3), ±(1 / Φ√3))
  • (±(1 / Φ√3), 0, ±(Φ / √3))
  • (±(Φ / √3), ±(1 / Φ√3), 0)
Type:
Source:
See:

(inner, constant) initialIco :Array.<vec3>

Twelve points of an icosahedron inscribed in the unit sphere.

Golden Ratio:
  • Φ = (√5+1)/2 = 1.618033988749895
Radius of circunsphere:
  • R = √(Φ² + 1)/2 a = 1
  • r = √(Φ² + 1) = 1.902113032590307 (a=2)
Edge length:
  • a = 2R / √(Φ² + 1) = 0.7639320225002103
Vertex Coordinates:
  • Φ / √(Φ² + 1)) = 0.85065080835204
  • 1 / √(Φ² + 1) = 0.5257311121191336
Twelve vertices:
  • (0, ±1/r, ±Φ/r)
  • (±1/r, ±Φ/r, 0)
  • (±Φ/r, 0, ±1/r)
Type:
Source:
See:

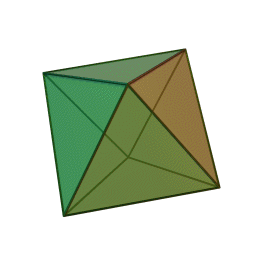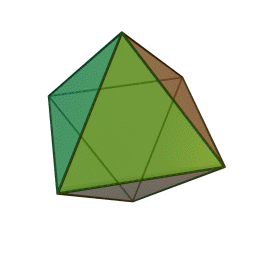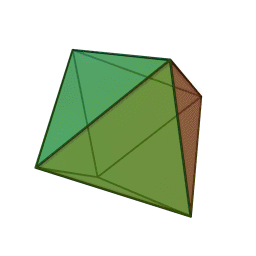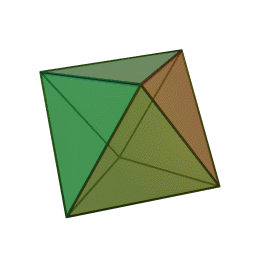
(inner, constant) initialOcta :Array.<vec3>

Six points of an octahedron inscribed in the unit sphere.

Radius of circunsphere:
  • R = √2/2 a = 1
Edge length:
  • a = 2R / √2 = 1.414213562373095
Six vertices:
  • (±1, 0, 0)
  • (0, ±1, 0)
  • (0, 0, ±1)
Type:
Source:
See:

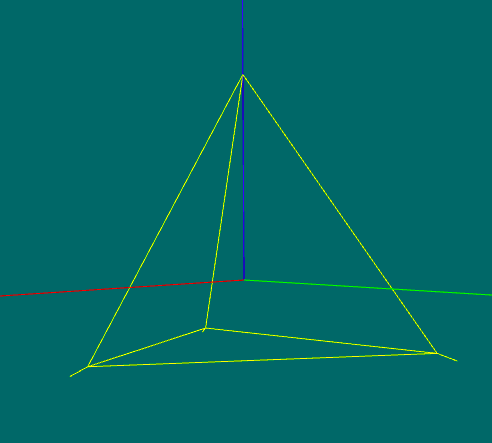
(inner, constant) initialTet :Array.<vec3>

Four points of a tetrahedron inscribed in the unit sphere, in three different vertex arrangements.

Radius of circunsphere:
  • R = √6 a/4 = 1
Radius of circuncircle:
  • r = a/√3 = 2/3 √6 / √3 = 2/3 √2 = √(8/9) = 0.9428090415820634
Edge length:
  • a = 4R / √6 = 2/3 √6 = 1.6329931618554523
Vertex coordinates:
  • x = r sin(π/6) = √(2/9) = 0.4714045207910317
  • y = r cos(π/6) = √(2/3) = 0.816496580927726
  • z = 1/3 = 0.3333333333333333 (24/9 = 8/9 + (z+1)²)
Four vertices, lower face parallell to the xy plane:
  • (r, 0, -z)
  • (-x, y, -z)
  • (-x, -y, -z)
  • (0, 0, 1)
Alternatively, higher face parallell to the xy plane:
  • (0, r, z)
  • (y, -x, z)
  • (-y, -x, z)
  • (0, 0, -1)
Embedded inside a cube:
  • (1/√3, 1/√3, 1/√3)
  • (-1/√3, -1/√3, 1/√3)
  • (-1/√3, 1/√3, -1/√3)
  • (1/√3, -1/√3, -1/√3)
Type:
Source:
See:

(inner) vec3 :glMatrix.vec3

gl-matrix 3 Dimensional Vector.
Type:
  • glMatrix.vec3
Source:

Methods

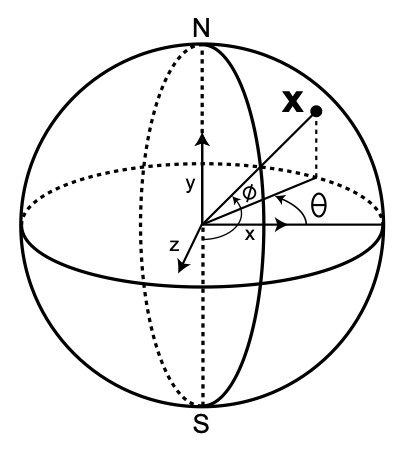
(static) cartesian2Spherical(p) → {Object.<s:Number, t:Number>}

Return a pair of spherical coordinates, in the range [0,1], corresponding to a point p onto the unit sphere.

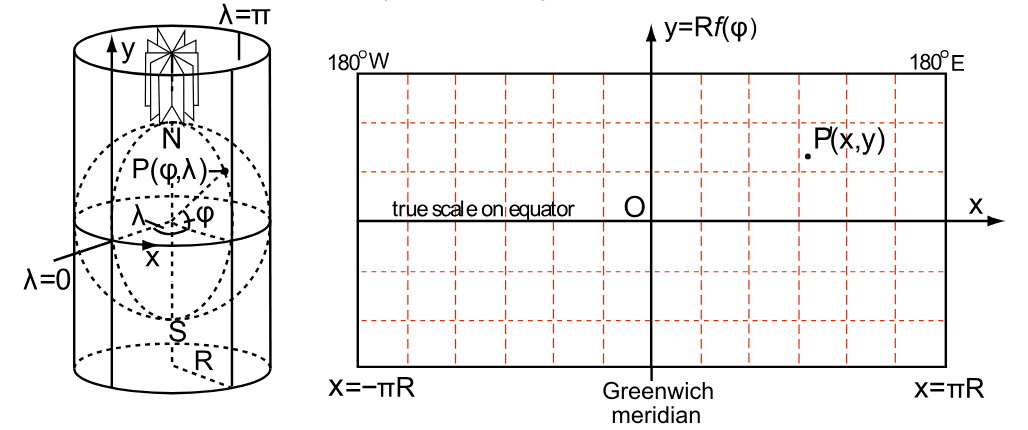
The forward projection transforms spherical coordinates into planar coordinates:
  • if point p is plotted on a plane, we have the plate carrée projection, a special case of the equirectangular projection.
  • this projection maps x to be the value of the longitude and y to be the value of the latitude.

The singularity of the mapping (parametrization) is at φ = 0 (y = -r) and φ = π (y = r):

  • In this case, an entire line at the top (or bottom) boundary of the texture is mapped onto a single point.
  • In geographic coordinate system, φ is measured from the positive y axis (North), not the z axis, as it is usual in math books.
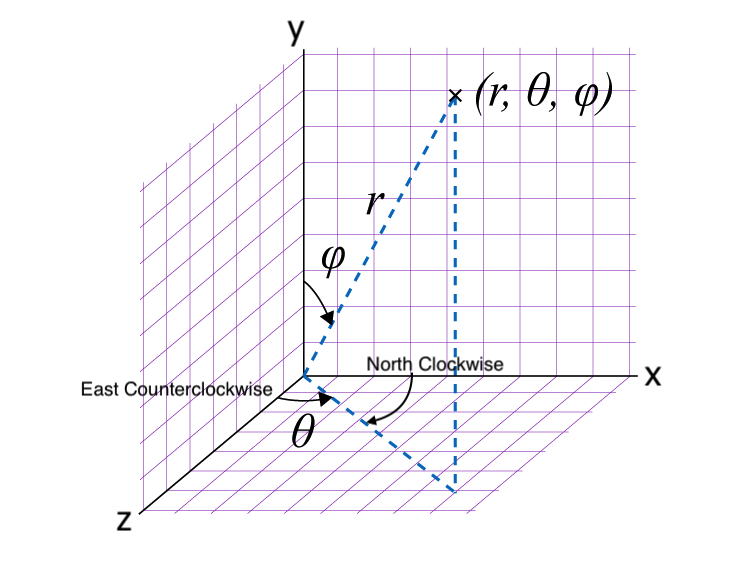
  • Therefore, we will use North-Counterclockwise Convention.
  • The 'clockwise from north' convention is used in navigation and mapping.
  • ________________________________________________
  • atan2(y, x) (East-Counterclockwise Convention)
  • atan2(x, y) (North-Clockwise Convention)
  • atan2(-x,-y) (South-Clockwise Convention)
  • ________________________________________________
  • cos(φ-90) = sin(φ)
  • sin(φ-90) = -cos(φ)
  • x = r cos(θ) sin(φ)
  • y = −r cos (φ)
  • z = -r sin(θ) sin(φ)
  • z/x = −(r sin(θ) sin(φ)) / (r cos(θ) sin(φ)) = -sin(θ) / cos(θ) = −tanθ
  • θ = atan(−z/x)
  • φ = acos(−y/r)
Note that this definition provides a logical extension of the usual polar coordinates notation,
with θ remaining the angle in the zx-plane and φ becoming the angle out of that plane.
Parameters:
Name Type Description
p vec3 a point on the sphere.
Source:
See:
Returns:
point p in spherical coordinates:
  • const [x, y, z] = p
  • r = 1 = √(x² + y² + z²)
  • s = θ = atan2(-z, x) / 2π + 0.5
  • t = φ = acos(-y/r) / π
  • tg(-θ) = -tg(θ) = tan (z/x)
  • arctan(-θ) = -arctan(θ) = atan2(z, x)
Since the positive angular direction is CCW, we can not use North-Clockwise Convention, because the image would be rendered mirrored.
  • border ≡ antimeridian
  • atan2(-z, x) (border at -x axis of the image - wrap left to right) (correct form) or
  • atan2(z, -x) (border at x axis of the image - wrap right to left).
  • atan2(z, x) (border at x axis of the image - mirrored).
Type
Object.<s:Number, t:Number>

(static) clamp(x, min, max) → {Number}

Constrain a value to lie between two further values.
Parameters:
Name Type Description
x Number value.
min Number minimum value.
max Number maximum value.
Source:
Returns:
min ≤ x ≤ max.
Type
Number

(static) mercator2Spherical(x, y) → {Object.<x:Number, y:Number>}

Convert a 2D point (x=long, y=lat) in mercator coordinates to a 2D point (θ, φ) in spherical coordinates.
  • θ = x + θ0, 0 ≤ x + θ0 ≤ 2π
  • φ = 2 atan (exp (y)) - π/2, -π ≤ y ≤ π → -85.051129° ≤ φ ≤ 85.051129°
Parameters:
Name Type Description
x Number longitude in [0,1].
y Number latitude in [0,1].
Source:
See:
Returns:
spherical coordinates in [0,1].
Type
Object.<x:Number, y:Number>

(static) pointsOnAntiMeridian(nopt) → {Float32Array}

Return an array with n points on the anti meridian.
Parameters:
Name Type Attributes Default Description
n Number <optional>
 nsegments number of points.
Source:
Returns:
points on the anti meridian.
Type
Float32Array

(static) pointsOnEquator(nopt) → {Float32Array}

Return an array with n points on the equator.
Parameters:
Name Type Attributes Default Description
n Number <optional>
 nsegments number of points.
Source:
Returns:
points on the equator.
Type
Float32Array

(static) pointsOnMeridian(longitudeopt, nopt, antiopt) → {Float32Array}

Return an array with n points on a meridian given its longitude.
Parameters:
Name Type Attributes Default Description
longitude Number <optional>
 0 distance east or west of the prime meridian: [-180°,180°]
n Number <optional>
 nsegments number of points.
anti Boolean <optional>
 false whether to draw the antimeridian also.
Source:
Returns:
points on the meridian.
Type
Float32Array

(static) pointsOnParallel(latitudeopt, nopt) → {Float32Array}

Return an array with n points on a parallel given its latitude.
Parameters:
Name Type Attributes Default Description
latitude Number <optional>
 0 distance north or south of the Equator: [-90°,90°].
n Number <optional>
 nsegments number of points.
Source:
Returns:
points on the parallel.
Type
Float32Array

(static) pointsOnPrimeMeridian(nopt) → {Float32Array}

Return an array with n points on the prime meridian.
Parameters:
Name Type Attributes Default Description
n Number <optional>
 nsegments number of points.
Source:
Returns:
points on the prime meridian.
Type
Float32Array

(static) radians(deg) → {Number}

Convert degrees to radians.
Parameters:
Name Type Description
deg Number angle in degrees.
Source:
Returns:
angle in radians.
Type
Number

(static) rotateUTexture(obj, degrees)

Rotate u texture coordinate by a given angle.
Parameters:
Name Type Description
obj module:polyhedron~polyData model data.
degrees Number rotation angle.
Source:

(static) setMercatorCoordinates(obj)

Set Mercator vertex coordinates.
Parameters:
Name Type Description
obj module:polyhedron~polyData model data.
Source:

(static) spherical2Cartesian(s, t, r) → {vec3}

Return a point on the unit sphere given their spherical coordinates: (θ, φ, r=1).

It is assumed that:
  • the two systems have the same origin,
  • the spherical reference plane is the Cartesian xz plane,
  • φ is inclination from the y direction, and
  • the azimuth is measured from the Cartesian x axis, so that the x axis has θ = 0° (prime meridian).
  • x = p[0] = r cos(θ) * sin(φ)
  • z = p[2] = -r sin(θ) * sin(φ)
  • y = p[1] = -r cos(φ)
Parameters:
Name Type Description
s Number azimuth angle θ, 0 ≤ θ ≤ 2π.
t Number zenith angle φ, 0 ≤ φ ≤ π.
r Number radius distance, r ≥ 0.
Source:
See:
Returns:
cartesian point onto the unit sphere.
Type
vec3

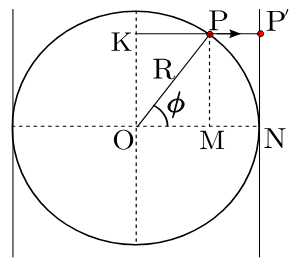
(static) spherical2Mercator(s, t) → {Object.<x:Number, y:Number>}

Convert a 2D point in spherical coordinates to a 2D point in Mercator coordinates.

The Mercator projection is a map projection that was widely used for navigation, since loxodromes are straight lines (although great circles are curved).

The following equations place the x-axis of the projection on the equator, and the y-axis at longitude θ0, where θ is the longitude and φ is the latitude:
  • x = θ - θ0, 0 ≤ θ - θ0 ≤ 2π
  • y = ln [tan (π/4 + φ/2)], -π/2 ≤ φ ≤ π/2 → -π ≤ y ≤ π
The poles extent to infinity. Therefore, to create a square image, the maximum latitude occurs at y = π, namely:
  • φmax = 2 atan (eπ) - π /2 = 85.051129°
As a consequence, we clamp the latitude to [-85°,85°] to avoid any artifact.
Parameters:
Name Type Description
s Number longitude (horizontal angle) θ, 0 ≤ θ ≤ 1.
t Number latitude (vertical angle) φ, 0 ≤ φ ≤ 1.
Source:
See:
Returns:
mercator coordinates in [0,1].
Type
Object.<x:Number, y:Number>

Type Definitions

polyData

An object containing raw data for vertices, normal vectors, texture coordinates, mercator coordinates and indices.

Polyhedra have no index.

Type:
  • Object
Properties:
Name Type Description
vertexPositions Float32Array vertex coordinates.
vertexNormals Float32Array vertex normals.
vertexTextureCoords Float32Array texture coordinates.
vertexMercatorCoords Float32Array mercator texture coordinates.
indices Uint16Array index array.
name String polyhedron name.
nfaces Number initial number of triangles.
maxNumSubdivisions Number maximum number of subdivisions.
ntri function return the number of triangles given the level of detail.
level function return the level of detail given the number of triangles.
Source: