Global

Members

axis :String

Current rotation axis.
Type:
  • String
Source:

axisBuffer :WebGLBuffer

Type:
  • WebGLBuffer
Source:

axisColorBuffer :WebGLBuffer

Type:
  • WebGLBuffer
Source:

(constant) axisColors :Float32Array

Axis colors.
Type:
  • Float32Array
Source:

(constant) axisVertices :Float32Array

Axis coordinates.
Type:
  • Float32Array
Source:

colorShader :WebGLShader

Handle to the compiled shader program on the GPU.
Type:
  • WebGLShader
Source:

(constant) eye :Array.<Number>

Camera position.
Type:
  • Array.<Number>
Source:

gl :WebGLRenderingContext

The OpenGL context.
Type:
  • WebGLRenderingContext
Source:

indexBuffer :WebGLBuffer

Type:
  • WebGLBuffer
Source:

lightingShader :WebGLShader

Handle to the compiled shader program on the GPU.
Type:
  • WebGLShader
Source:

lineBuffer :WebGLBuffer

Handle to a buffer on the GPU.
Type:
  • WebGLBuffer
Source:

lines :Float32Array

Array with edges end points.
Type:
  • Float32Array
Source:

modelMatrix :Matrix4

Model transformation matrix.
Type:
Source:

mscale :Number

Scale applied to a model to make its size adequate for rendering.
Type:
  • Number
Source:

normal :Float32Array

Array with normal end points.
Type:
  • Float32Array
Source:

normalBuffer :WebGLBuffer

Type:
  • WebGLBuffer
Source:

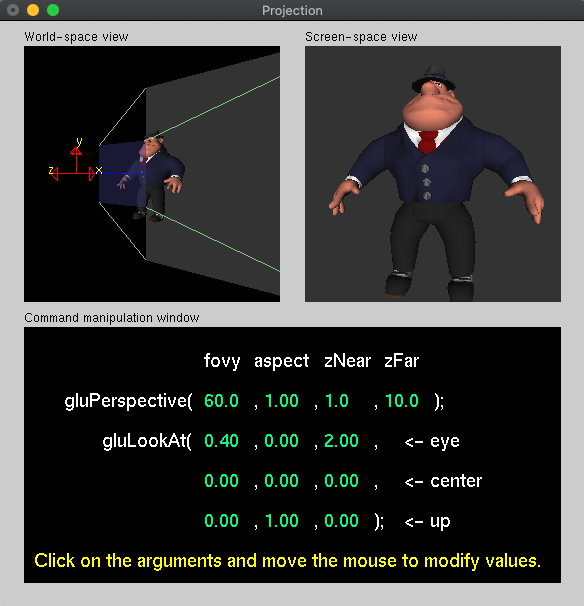
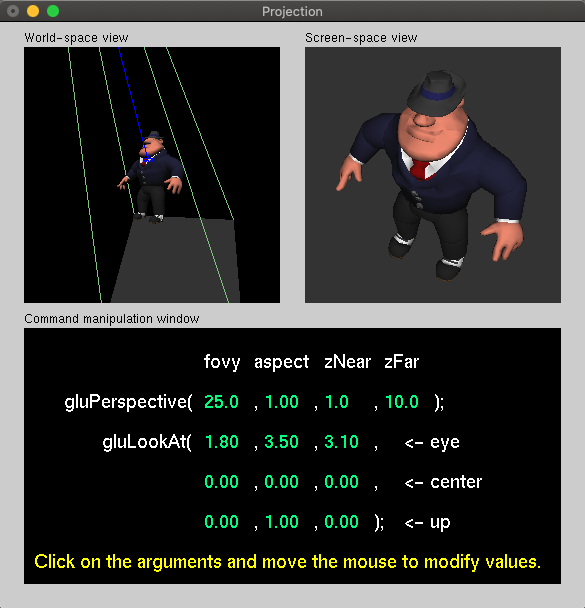
(constant) projection :Matrix4

For projection, we can either use:

  • An orthographic projection, specifying the clipping volume explicitly:
    • const projection = new Matrix4().setOrtho(-1.5, 1.5, -1, 1, 4, 6);
  • Or the same perspective projection, using the Frustum function with:
    • a 30 degree field of view, and a near plane at 4,
      which corresponds to a view plane height of: 4 * tan(15) = 1.07
    • const projection = new Matrix4().setFrustum(-1.5 * 1.07, 1.5 * 1.07, -1.07, 1.07, 4, 6);
  • Or a perspective projection specified with a field of view, an aspect ratio, and distance to near and far clipping planes:
    • const projection = new Matrix4().setPerspective(30, 1.5, 0.1, 1000);
Here use aspect ratio 3/2 corresponding to canvas size 900 x 600

Type:
Source:

rotator :SimpleRotator

Arcball.
Type:
Source:

(constant) selector :Object

Turn the display of the model mesh/texture/axes/animation on/off.
Type:
  • Object
Properties:
Name Type Description
lines Boolean mesh visible/invisible
texture Boolean model surface visible/invisible
axes Boolean axes visible/invisible
paused Boolean animation on/off
Source:

(constant) teapotModel :modelData

An IFS of the famous teapot, about 20 units big.
Type:
Source:

theModel :modelData

Our model data.
Type:
Source:

vertexBuffer :WebGLBuffer

Handle to a buffer on the GPU.
Type:
  • WebGLBuffer
Source:

vertexNormalBuffer :WebGLBuffer

Type:
  • WebGLBuffer
Source:

(constant) viewDistance :Number

View distance.
Type:
  • Number
Source:

(constant) viewMatrix :Matrix4

View matrix.

One strategy is to identify a transformation to our camera frame then invert it.
Therefore, the camera transformation takes (0,0,0) to the camera position. 
   rotate(30, 0, 1, 0) * rotate(-45, 1, 0, 0) * translate(0, 0, 5)

   camera transformation:
       0.8660253882408142 -0.3535533845424652 0.3535533845424652 1.7677669525146484
       0                   0.7071067690849304 0.7071067690849304 3.535533905029297
      -0.5                -0.6123723983764648 0.6123723983764648 3.061861991882324
       0                   0                   0                 1

   translate(0, 0, -5) * rotate(45, 1, 0, 0) * rotate(-30, 0, 1, 0)

   view matrix:
       0.8660253882408142 0                  -0.5                 0
      -0.3535533845424652 0.7071067690849304 -0.6123723983764648  0
       0.3535533845424652 0.7071067690849304  0.6123723983764648 -5
       0                  0                   0                   1
The view matrix is the inverse of the camera's transformation matrix: viewMatrix = camera ⁻¹.
  • The camera's transformation matrix takes something that's local to the camera and transforms it to world space
    (transforming the point [0,0,0] will give you the camera's position)
  • The view matrix takes something that's in world space and transforms it so that it's local to the camera
    (transforming the camera's position will give you [0, 0, 0])

LookAt functions from math libraries are just a convenience, indeed, and requires a view point, a point to look at, and a direction "up", for camera orientation:

The approximate view point here is: [1.77, 3.54, 3.06]

   const viewMatrix = new Matrix4().setLookAt(
     ...eye,   // view point
     0, 0, 0,  // at - looking at the origin
     0, 1, 0); // up vector - y axis

or using the glmatrix package

   const viewMatrix = mat4.lookAt(
     [],         // mat4 frustum matrix will be written into
     eye,        // view point
     [0, 0, 0],  // look at (center)
     [0, 1, 0]); // view up
Type:
Source:
See:

yNorth :Boolean

Sets the North to be the y-axis, so the z-axis points outside the screen.
Type:
  • Boolean
Source:

Methods

animate() → {loop}

A closure to define an animation loop.
Source:
Returns:
Type
loop

createEvent(key) → {KeyboardEvent}

Returns a new keyboard event.
Parameters:
Name Type Description
key String char code.
Source:
Returns:
a keyboard event.
Type
KeyboardEvent

createModel(shape, chi) → {modelData}

Sets up all buffers for the given (triangulated) model (shape).

Uses the webgl vertex buffer, normal buffer, texture buffer and index buffer, created in mainEntrance.
Then, binds each one of them as an array buffer and copies the corresponding shape array data to them.

Also, the Euler characteristic for the model is:

  • χ = 2 − 2g − b
for a surface with g handles and b boundaries.

The number of triangles must be even for a valid triangulation of the sphere:

  • V - E + T = 2 (sphere)
  • V - E + T = 0 (torus)
Parameters:
Name Type Default Description
shape modelData a BREP model given as an IFS.
chi Number | null 2 model Euler Characteristic.
Source:
See:
Returns:
shape.
Type
modelData

createProgram(gl, vshader, fshader) → {WebGLProgram}

Create the linked program object
Parameters:
Name Type Description
gl WebGLRenderingContext GL context.
vshader String a vertex shader program.
fshader String a fragment shader program.
Source:
See:
Returns:
created program object, or null if the creation has failed.
Type
WebGLProgram

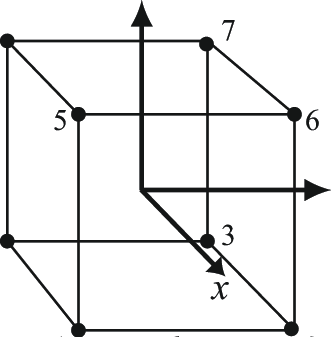
cube(side) → {modelData}

Create a model of a cube, centered at the origin.

This is not a particularly good format for a cube, since an IFS representation has a lot of redundancy.
Parameters:
Name Type Description
side Number the length of a side of the cube. If not given, the value will be 1.
Source:
Returns:
Type
modelData

draw()

Code to actually render our geometry.

Draw axes, model, and lines.
Source:

drawAxes()

Draws the axes.

Uses the colorShader.
Source:

drawLines()

Draws the mesh edges and normals.

Uses the colorShader.
Source:

drawModel()

Draws the model, by using the lightingShader.

If theModel.indices is defined, then calls drawElements. Otherwise, drawArrays.

Since three.js version 125, THREE.Geometry was deprecated and replaced by THREE.BufferGeometry, which always define indices for efficiency.

Source:

getChar(event) → {String}

Translate keypress events to strings.
Parameters:
Name Type Description
event KeyboardEvent key pressed.
Source:
See:
Returns:
typed character.
Type
String

getModelData(geom) → {modelData}

Given an instance of returns an object containing raw data for vertices, normal vectors, texture coordinates, and indices.

Polyhedra have no index.

Parameters:
Name Type Description
geom THREE.BufferGeometry THREE.BoxGeometry
THREE.CapsuleGeometry,
THREE.ConeGeometry,
THREE.CylinderGeometry,
THREE.PlaneGeometry,
THREE.RingGeometry,
THREE.SphereGeometry,
THREE.TorusGeometry,
THREE.TorusKnotGeometry,
THREE.DodecahedronGeometry,
THREE.IcosahedronGeometry,
THREE.OctahedronGeometry,
THREE.TetrahedronGeometry,
THREE.TeapotGeometry.
Source:
Returns:
Type
modelData

getModelMatrix() → {Matrix4}

Returns a new scale model matrix, which applies mscale.
Source:
Returns:
model matrix.
Type
Matrix4

getWebGLContext(canvas, opt_debug) → {WebGL2RenderingContext}

Initialize and get the rendering context for WebGL. This will make any GL errors show up in your browser JavaScript console.
Parameters:
Name Type Description
canvas HTMLCanvasElement <canvas> element.
opt_debug Boolean flag to initialize the context for debugging.
Deprecated:
  • since WebGL2
Source:
See:
Returns:
the rendering context for WebGL.
Type
WebGL2RenderingContext

handleKeyPress(event) → {key_event}

Closure for keydown events.

Chooses a model and which axis to rotate around.
Parameters:
Name Type Description
event KeyboardEvent keyboard event.
Source:
Returns:
callback for handling a keyboard event.
Type
key_event

initShaders(GL, vshader, fshader) → {Boolean}

Create a program object and make it current.
Parameters:
Name Type Description
GL WebGLRenderingContext context.
vshader String a vertex shader program.
fshader String a fragment shader program.
Source:
Returns:
true, if the program object was created and successfully made current.
Type
Boolean

loadShader(gl, type, source) → {WebGLShader}

Create a shader object
Parameters:
Name Type Description
gl WebGLRenderingContext GL context.
type gl.VERTEX_SHADER | gl.FRAGMENT_SHADER the type of the shader object to be created,
source DOMString shader program.
Source:
See:
Returns:
created shader object, or null if the creation has failed.
Type
WebGLShader

mainEntrance()

Entry point when page is loaded.

Load all data into the buffers (just once) before proceeding.
Source:
See:

makeCube(create_indices) → {Object}

Creates a unit cube, centered at the origin, and set its properties: vertices, normal vectors, texture coordinates, indices and colors.

For a proper specular reflection on planar faces, such as a cube or a polyhedron, the normal vectors have to be perpendicular to the plane of each face.

Computing an average normal, like is done here when creating indices, is what one would want to do for a smooth object like a sphere.

The resulting rendering is very unpleasant, in this case. The right course is creating three duplicate vertices per cube corner.

Even if cube.indices is not defined here, drawModel can handle it.

Parameters:
Name Type Default Description
create_indices Boolean false whether to generated vertex indices or not.
Properties:
Name Type Description
cube.numVertices Number number of vertices (36).
cube.vertices Float32Array vertex coordinate array (108 = 36 * 3).
cube.normals Float32Array vertex normal array (108 = 36 * 3).
cube.colors Float32Array vertex color array (144 = 36 * 4).
cube.texCoords Float32Array vertex texture array (72 = 36 * 2).
cube.indices Uint16Array vertex index array (36 = 6 * 2 * 3).
Source:
See:
Returns:
cube
Type
Object

makeNormalMatrixElements(model, view) → {Float32Array}

Matrix for taking normals into eye space.

Returns a matrix to transform normals, so they stay perpendicular to surfaces after a linear transformation.
Parameters:
Name Type Description
model Matrix4 model matrix.
view Matrix4 view matrix.
Source:
See:
Returns:
3x3 normal matrix (transpose inverse) from the 4x4 modelview matrix.
Type
Float32Array

ring(innerRadius, outerRadius, slices) → {modelData}

Creates a model of an annulus or disk lying in the xy plane, centered at the origin.

This is not a great representation, since all the normals are the same.
Parameters:
Name Type Description
innerRadius Number the radius of the hole in the radius; a value of zero will give a disk rather than a ring.
If ommited, the default value is 0.25.
outerRadius Number the radius of the ring, from the center to the outer edge. Must be greater than innerRadius.
If ommited, the default value is 2*innerRadius if innerRadius > 0 or 0.5 otherwise.
slices Number the number of radial subdivisions in the circular approximation of an annulus, minimum 3, default 32.
Source:
Returns:
Type
modelData

selectModel()

Selects a model from a menu.
Source:

setNorth(vertices, normals)

Rotate the given model so the y-axis points North.

The variable yNorth must be true, otherwise this function has no effect:
  • if (yNorth) (x, y, z) → (-x, z , y)
Parameters:
Name Type Description
vertices Float32Array vertex array.
normals Float32Array normal array.
Source:

uvCone(radius, height, slices, stacks, noBottom) → {modelData}

Defines a model of a cone.

The axis of the cone is the z-axis, and the center is at (0,0,0).
Parameters:
Name Type Description
radius Number the radius of the cone
height Number the height of the cone. The cone extends from -height/2 to height/2 along the z-axis, with the tip at (0,0,height/2).
slices Number the number of slices, like the slices of an orange, minimum 3, default 32.
stacks Number the number of stacks, like horizontal cuts of an orange, minimum 1, default 16.
noBottom Boolean if missing or false, the cone has a bottom; if set to true, the cone does not have a bottom.
The bottom is a disk at the wide end of the cone.
Source:
See:
Returns:
Type
modelData

uvCylinder(radius, height, slices, stacks, noTop, noBottom) → {modelData}

Defines a model of a cylinder.

The axis of the cylinder is the z-axis, and the center is at (0,0,0).
Parameters:
Name Type Description
radius Number the radius of the cylinder
height Number the height of the cylinder.
The cylinder extends from -height/2 to height/2 along the z-axis.
slices Number the number of slices, like the slices of an orange, minimum 3, default 32.
stacks Number the number of stacks, like horizontal cuts of an orange, minimum 1, default 16.
noTop Boolean if missing or false, the cylinder has a top; if set to true, the cylinder does not have a top.
The top is a disk at the positive end of the cylinder.
noBottom Boolean if missing or false, the cylinder has a bottom; if set to true, the cylinder does not have a bottom.
The bottom is a disk at the negative end of the cylinder.
Source:
See:
Returns:
Type
modelData

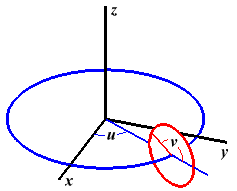
uvSphere(radius, slices, stacks) → {modelData}

Create a model of a sphere.

The z-axis is the axis of the sphere with the north pole on the positive z-axis and the center at (0,0,0).

The number of triangles is 2 * slices * stacks, e.g., 48 * 24 * 2 = 2304.

However, two rows and one column of vertices have been duplicated. Without vertex duplication, the number of triangles would be 48 * 23 * 2 = 2208.
In fact, this is topologically a cylinder whose vertices on the two borders have the same coordinates of the sphere north/south poles, respectively:

  • uvSphere(radius, slices, stack) ≍ uvCylinder(r, height, slices, stack, true, true)

Parameters:
Name Type Description
radius Number the radius of the sphere, default 0.5 if not specified.
slices Number the number of lines of longitude, minimum 3, default 32
stacks Number the number of lines of latitude plus 1, minimum 2, default 16.
(This is the number of vertical slices, bounded by lines of latitude, the north pole and the south pole.)
Source:
See:
Returns:
Type
modelData

uvSphereND(radius, slices, stacks) → {modelData}

Create a model of a sphere.

The z-axis is the axis of the sphere with the north pole on the positive z-axis and the center at (0,0,0).

This version does not duplicate vertices on the seam, but it does require Tarini's method when texturing.

Parameters:
Name Type Description
radius Number the radius of the sphere, default 0.5 if not specified.
slices Number the number of lines of longitude, minimum 3, default 32
stacks Number the number of lines of latitude plus 1, minimum 2, default 16.
(This is the number of vertical slices, bounded by lines of latitude, the north pole and the south pole.)
Source:
See:
Returns:
Type
modelData

uvTorus(outerRadius, innerRadius, slices, stacks) → {modelData}

Create a model of a torus (surface of a doughnut).

The z-axis goes through the doughnut hole, and the center of the torus is at (0,0,0).
Parameters:
Name Type Description
outerRadius Number the distance from the center to the outside of the tube, 0.5 if not specified.
innerRadius Number the distance from the center to the inside of the tube, outerRadius/3 if not specified.
(This is the radius of the doughnut hole.)
slices Number the number of lines of longitude, minimum 3, default 32.
These are slices parallel to the z-axis and go around the tube the short way (through the hole).
stacks Number the number of lines of latitude plus 1, minimum 2, default 16.
These lines are perpendicular to the z-axis and go around the tube the long way (around the hole).
Source:
See:
Returns:
Type
modelData

vecLen(v) → {Number}

Returns the magnitude (length) of a vector.
Parameters:
Name Type Description
v Array.<Number> n-D vector.
Source:
See:
Returns:
vector length.
Type
Number

Type Definitions

key_event(event)

Handler for keydown events.

Parameters:
Name Type Description
event KeyboardEvent keyboard event.
Source:

loop()

Callback to keep drawing frames.
Source:
See:

modelData

An object containing raw data for vertices, normal vectors, texture coordinates, and indices.

Polyhedra have no index.

Type:
  • Object
Properties:
Name Type Description
vertexPositions Float32Array vertex coordinates.
vertexNormals Float32Array vertex normals.
vertexTextureCoords Float32Array texture coordinates.
indices Uint16Array | Uint32Array index array.
Source:

Events

clickArrowDown

Animates the object, by generating an "↓" event, whenever the Arrow Down button is clicked.
Source:
See:

clickArrowUp

Animates the object, by generating an "↑" event, whenever the Arrow Up button is clicked.
Source:
See:

clickMesh

Draws the mesh and vertex normals, by generating an "l" event, whenever the Mesh button is clicked.
Source:
See:

clickRot

Animates the object, by generating an " " event, whenever the Rotate button is clicked.
Source:
See:

keydown

Key handler.

Calls handleKeyPress whenever any of these keys is pressed:
  • Space
  • x, y, z
  • p, s, T, o
  • a, k, l
Source:
See:

load

Loads the application.
Source:
See: